对涂鸦进行分类的循环神经网络
Quick, Draw! 是一个涂鸦游戏,玩家需要画出一系列物体,看电脑能否识别。
Quick, Draw! 的识别功能由一个分类器完成,其输入是玩家的涂鸦,由一连串的笔画(笔画由一系列点的坐标构成)组成,输出则是涂鸦所对应的物体类别。
在这个教程中,我们将会展示如何为这个游戏构建一个基于 RNN (循环神经网络)的分类器。模型将会使用卷积层、LSTM 层以及一个 softmax 输出层来分辨涂鸦的类别。
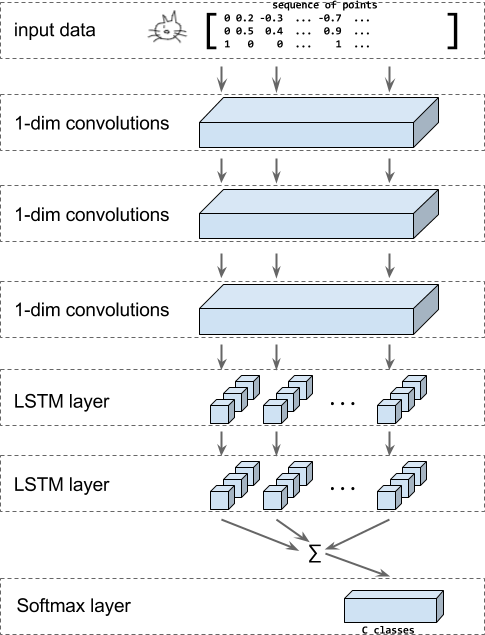
上图展示了此教程中构建的模型架构。输入为一个图形,编码为由 x, y 和 n 构成的坐标点序列,其中 n 表示该点是否是新笔划中的第一个点。
然后,应用一系列一维卷积,然后使用 LSTM 层将所有的输出传递给 softmax 层,进而进行涂鸦分类。
此教程使用的数据来自实际的 Quick, Draw! 游戏公开数据集。数据包含了 50M 个涂鸦以及 345 个分类。
运行教程代码
运行这个教程的代码:
- 安装 TensorFlow
- 下载教程代码。
下载
TFRecord格式的数据 并解压。更多细节请参考可选:下载整个 Quick Draw 数据 以及如何转换原始 Quick, Draw! 数据。使用一下命令可以执行教程代码,并训练教程中描述的 RNN 模型。请自行填写在第三步中放置的解压好的数据路径。
python train_model.py \
--training_data=rnn_tutorial_data/training.tfrecord-?????-of-????? \
--eval_data=rnn_tutorial_data/eval.tfrecord-?????-of-????? \
--classes_file=rnn_tutorial_data/training.tfrecord.classes
教程细节
下载数据
我们将本教程使用的数据作为包含 TFExamples 的 TFRecord 文件提供下载:
http://download.tensorflow.org/data/quickdraw_tutorial_dataset_v1.tar.gz
或者,你也可以从 Google 云上下载 ndjson 格式的原始数据,并将其转换为包含 TFExamples 的 TFRecord 文件,具体方法参考下一节。
可选:下载整个 Quick Draw 数据
完整的 Quick, Draw! 数据集 可以在 Google Cloud Storage 上下载按类别分类的 ndjson 格式原始文件。你可以在Cloud Console 上直接浏览文件列表。
要下载我们推荐的数据,请使用 gsutil 下载整个数据集。注意,原始 .ndjson 格式的文件大约有 22GB。
然后使用下面的命令检查你的 gsutil 安装是否正常,并且可以访问到数据存储区:
gsutil ls -r "gs://quickdraw_dataset/full/simplified/*"
其输出是一长串文件列表,如下所示:
gs://quickdraw_dataset/full/simplified/The Eiffel Tower.ndjson
gs://quickdraw_dataset/full/simplified/The Great Wall of China.ndjson
gs://quickdraw_dataset/full/simplified/The Mona Lisa.ndjson
gs://quickdraw_dataset/full/simplified/aircraft carrier.ndjson
...
然后,创建一个文件夹并从云端下载数据集:
mkdir rnn_tutorial_data
cd rnn_tutorial_data
gsutil -m cp "gs://quickdraw_dataset/full/simplified/*" .
这个将下载大约 23GB 数据并持续很长一段时间。
可选:数据转换
python create_dataset.py --ndjson_path rnn_tutorial_data \
--output_path rnn_tutorial_data
下面描述更为详细的转换过程。
原始的 QuickDraw 数据格式为 .ndjson,每行包含一个 JSON 对象,例如:
{"word":"cat",
"countrycode":"VE",
"timestamp":"2017-03-02 23:25:10.07453 UTC",
"recognized":true,
"key_id":"5201136883597312",
"drawing":[
[
[130,113,99,109,76,64,55,48,48,51,59,86,133,154,170,203,214,217,215,208,186,176,162,157,132],
[72,40,27,79,82,88,100,120,134,152,165,184,189,186,179,152,131,114,100,89,76,0,31,65,70]
],[
[76,28,7],
[136,128,128]
],[
[76,23,0],
[160,164,175]
],[
[87,52,37],
[175,191,204]
],[
[174,220,246,251],
[134,132,136,139]
],[
[175,255],
[147,168]
],[
[171,208,215],
[164,198,210]
],[
[130,110,108,111,130,139,139,119],
[129,134,137,144,148,144,136,130]
],[
[107,106],
[96,113]
]
]
}
根据我们需要创建分类器的目的, 我们只关心字段 word 和 drawing。因此,在解析 .ndjson 文件时,我们逐行将 JSON 通过一个函数将 drawing 字段处理成 [number_of_points, 3] 大小的张量,并同时返回类别的名称。
def parse_line(ndjson_line):
"""解析一个 ndjson 行,并返回涂鸦数据和类别名称."""
sample = json.loads(ndjson_line)
class_name = sample["word"]
inkarray = sample["drawing"]
stroke_lengths = [len(stroke[0]) for stroke in inkarray]
total_points = sum(stroke_lengths)
np_ink = np.zeros((total_points, 3), dtype=np.float32)
current_t = 0
for stroke in inkarray:
for i in [0, 1]:
np_ink[current_t:(current_t + len(stroke[0])), i] = stroke[i]
current_t += len(stroke[0])
np_ink[current_t - 1, 2] = 1 # stroke_end
# 预处理.
# 1. 大小归一
lower = np.min(np_ink[:, 0:2], axis=0)
upper = np.max(np_ink[:, 0:2], axis=0)
scale = upper - lower
scale[scale == 0] = 1
np_ink[:, 0:2] = (np_ink[:, 0:2] - lower) / scale
# 2. 计算方差
np_ink = np_ink[1:, 0:2] - np_ink[0:-1, 0:2]
return np_ink, class_name
由于我们希望将读取的数据随机打乱,因此我们按随机顺序将每个类别文件读取并写入到随机分片中。
对于训练数据而言,我们每个类别读取 10000 个样本,而对于测试样本而言,我们对每个类别读取 1000 个样本。
然后将这些数据重新格式化为形状为 [num_training_samples, max_length, 3] 的张量。然后再根据坐标值确定原始图形的边框,并将尺寸标准化,使图形具有单位长度的大小。
最后,我们计算连续点之间的差值并将其作为 VarLenFeature 存储在 tensorflow.Example 下,命名为 ink 字段。此外,我们还将 class_index 作为单个 FixedLengthFeature 条目进行存储,ink 的 shape 作为长度为 2 的 FixedLengthFeature 进行存储。
定义模型
构建模型分为以下几步:
将输入数据的形状进行变换,即把数据的小批量填充为其内容的最大程度。除了涂鸦轨迹数据外,我们还需要每个样本的类别以及长度。这需要函数
_get_input_tensors进行处理。将输入传递给
_add_conv_layers中一系列卷积层。将卷积层输出的结果传递给
_add_rnn_layers中一系列的双向 LSTM 层。最后将每个时间点得到的输出求和得到一个固定长度的输入数据的向量。使用
_add_fc_layers中的 softmax 图层对此向量进行分类。
代码如下:
inks, lengths, targets = _get_input_tensors(features, targets)
convolved = _add_conv_layers(inks)
final_state = _add_rnn_layers(convolved, lengths)
logits =_add_fc_layers(final_state)
_get_input_tensors
为了获得输入特征,我们首先需要从特征字典中获取并创建一个包含输入序列长度的一维张量,大小为 [batch_size]。用户所绘内容作为稀疏张量存储在字典中,我们再将其转换为一个稠密张量,大小为 [batch_size, ?, 3]。最后,如果目标通过了,我们就确保其存储在一个尺寸为 [batch_size] 的一维张量中。
代码如下:
shapes = features["shape"]
lengths = tf.squeeze(
tf.slice(shapes, begin=[0, 0], size=[params["batch_size"], 1]))
inks = tf.reshape(
tf.sparse_tensor_to_dense(features["ink"]),
[params["batch_size"], -1, 3])
if targets is not None:
targets = tf.squeeze(targets)
_add_conv_layers
卷积层的数量和滤波器的长度通过 params 字典中的 num_conv 和 conv_len 来进行配置。
输入是一个三维的序列,我们将会使用一维的卷积操作,所以我们把第三维的数据看做是图像的色彩通道。这意味着输入的形状为 [batch_size, length, 3],那么输出的张量形状则会是 [batch_size, length, number_of_filters]。
convolved = inks
for i in range(len(params.num_conv)):
convolved_input = convolved
if params.batch_norm:
convolved_input = tf.layers.batch_normalization(
convolved_input,
training=(mode == tf.estimator.ModeKeys.TRAIN))
# 如果启用了 dropout,则在除第一层以外的卷积层后增加 dropout 层
if i > 0 and params.dropout:
convolved_input = tf.layers.dropout(
convolved_input,
rate=params.dropout,
training=(mode == tf.estimator.ModeKeys.TRAIN))
convolved = tf.layers.conv1d(
convolved_input,
filters=params.num_conv[i],
kernel_size=params.conv_len[i],
activation=None,
strides=1,
padding="same",
name="conv1d_%d" % i)
return convolved, lengths
_add_rnn_layers
我们将卷积输出传递给双向 LSTM 层,为此我们使用了 contrib 的辅助函数。
outputs, _, _ = contrib_rnn.stack_bidirectional_dynamic_rnn(
cells_fw=[cell(params.num_nodes) for _ in range(params.num_layers)],
cells_bw=[cell(params.num_nodes) for _ in range(params.num_layers)],
inputs=convolved,
sequence_length=lengths,
dtype=tf.float32,
scope="rnn_classification")
你可以阅读源码来了解如何使用 CUDA 以加速计算的实现。
我们对 LSTM 的结果进行求和得到一个密集的固定长度的向量。笔画序列被填充为 0 的部分不参与到结果的计算之中。
mask = tf.tile(
tf.expand_dims(tf.sequence_mask(lengths, tf.shape(outputs)[1]), 2),
[1, 1, tf.shape(outputs)[2]])
zero_outside = tf.where(mask, outputs, tf.zeros_like(outputs))
outputs = tf.reduce_sum(zero_outside, axis=1)
添加全连接层
输入的编码将交给一个全连接层,随后我们再将其输出交给 softmax 层。
tf.layers.dense(final_state, params.num_classes)
损失函数,预测以及优化器
最后,我们需要设置损失函数、训练操作以及模型预测来完成 ModelFn 的构建:
cross_entropy = tf.reduce_mean(
tf.nn.sparse_softmax_cross_entropy_with_logits(
labels=targets, logits=logits))
# 添加优化器
train_op = tf.contrib.layers.optimize_loss(
loss=cross_entropy,
global_step=tf.train.get_global_step(),
learning_rate=params.learning_rate,
optimizer="Adam",
# 梯度截断可以提升训练开始时的稳定性
clip_gradients=params.gradient_clipping_norm,
summaries=["learning_rate", "loss", "gradients", "gradient_norm"])
predictions = tf.argmax(logits, axis=1)
return model_fn_lib.ModelFnOps(
mode=mode,
predictions={"logits": logits,
"predictions": predictions},
loss=cross_entropy,
train_op=train_op,
eval_metric_ops={"accuracy": tf.metrics.accuracy(targets, predictions)})
训练和评估模型
我们使用 Estimator 和 Experiment 的 API 来方便地训练和评估我们的模型:
estimator = tf.estimator.Estimator(
model_fn=model_fn,
model_dir=output_dir,
config=config,
params=model_params)
# 训练模型
tf.contrib.learn.Experiment(
estimator=estimator,
train_input_fn=get_input_fn(
mode=tf.contrib.learn.ModeKeys.TRAIN,
tfrecord_pattern=FLAGS.training_data,
batch_size=FLAGS.batch_size),
train_steps=FLAGS.steps,
eval_input_fn=get_input_fn(
mode=tf.contrib.learn.ModeKeys.EVAL,
tfrecord_pattern=FLAGS.eval_data,
batch_size=FLAGS.batch_size),
min_eval_frequency=1000)
这篇教程旨在帮助你熟悉循环神经网络的 API 以及评估器的使用,因而只是在一个比较小的数据集上进行了实验。如果使用更大的数据集的话,模型会取得更加优异的表现。
训练一百万步之后,你应该能够得到一个准确率约为 70% 的模型。这个结果足以来构建一个快速涂鸦游戏了,因为玩家能够不断地调整他的画作直到被识别。同时,这个游戏不一定要求模型给出完全正确的判断,而只要对应类别的概率高于一定的阈值,就认可玩家的涂鸦。